
Выбор редакции
Проекты
Сильнее, чем миллион. О Григории Перельмане

А.: Гриша Перельман заставил всех нас (ну, или скажем, многих) пережить несколько дискомфортных минут, когда отказался от причитающегося ему миллиона долларов США. Но со временем его поступок выглядит все более вдохновляющим.
В.: да он же потом вроде забрал его, миллиен то? не помню где уж слыхал, но там у него женсчина появилась и она его "убедила" забрать деньги:-)
А.: я не слышал, что он взял таки мильон; в самом деле?
H.: взял, мама уговорила!
A.: да, миллион - это сила
(Из разговора в ФБ. Орфография и пунктуация подлинника сохранены.)
Впервые я узнал о Григории Перельмане 4 июня 2003 года. В этот день на сайте “Русского журнала” появился перевод статьи Джордана Элленберга “Математика - дело молодых?”, где очень коротко рассказывалось о гипотезе Пуанкаре и премии Института Клэя (The Clay Mathematics Institute of Cambridge, Massachusetts, The Millennium Prize Problems) размером в миллион долларов, которая за это доказательство обещана. (Оригинал статьи: Is Math a Young Man's Game? No. Not every mathematician is washed up at 30. By Jordan Ellenberg)
То, что эту статью переводил человек (переводчик не указан), имеющий весьма слабое представление о математике, было ясно сразу. Перевести "simply connected" словами "просто соединенное", как это сделано в РЖ, нельзя, потому что есть простой русский аналог этого термина: “односвязное”. Ну это ладно. Это мелочи. Но я не поверил Элленбергу. Я не поверил, что некий русский математик Григорий Перельман, прочитавший в MIT цикл лекций, действительно изложил доказательство гипотезы Пуанкаре. Ну мало ли какой Перельман какие читал лекции в MIT? Придут серьезные мужчины, все проверят и обязательно найдут ошибку. Гипотеза уже сто лет стоит, как скала, и даже подходов не видно. Но известие это мне в голову запало. Может, потому что других статей о математике в РЖ я не встречал. Может, потому что книжки Якова Перельмана читал в детстве и очень любил. Потом стали поступать новые известия. И то, что казалось невероятным, сначала стало правдоподобным, а потом - несомненным.
Григорий Перельман и доказательство гипотезы Пуанкаре. Краткая хронология событий
11 ноября 2002 года. Григорий Перельман, известный российский математик, работающий в Санкт-Петербургском отделении Математического института РАН им. Стеклова, разместил на сайте arXiv.org (этот сайт предназначен для размещения статей, ожидающих публикации в реферируемом журнале) статью "The entropy formula for the Ricci flow and its geometric applications". Она посвящена доказательству гипотезы геометризация Уильяма Тёрстона.
12 ноября 2002 года дюжина американских математиков получила от Перельмана по email краткое изложение опубликованной статьи. Все эти математики в большей или меньшей степени участвовали в исследованиях, связанных с гипотезой Пуанкаре. Сама гипотеза даже не упоминается в названии статьи, но все поняли, о чем, собственно, идет речь. Перельмана многие знали лично, поскольку он работал в Соединенных Штатах в начале 1990-х, но потом, несмотря на многочисленные очень привлекательные во всех отношениях (в том числе и финансовых) предложения, вернулся в Санкт-Петербург. Публикация Перельмана вызвала живейший интерес. Но изложение оказалось довольно трудным для понимания. Даже крупнейшим специалистам-геометрам пришлось всерьез задуматься. И они задумались, но очень по-разному.
10 марта 2003 года на arXiv.org появилась вторая статья Перельмана, посвященная той же теме.
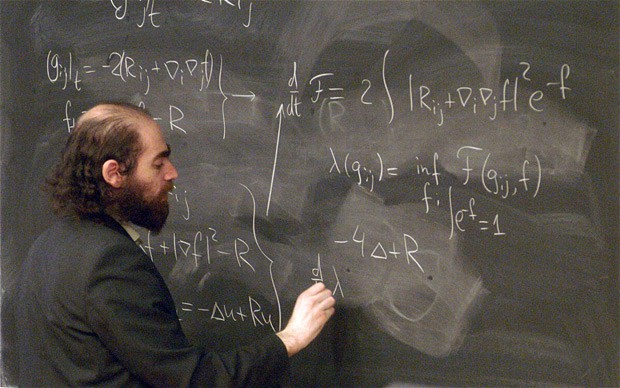
Апрель 2003-го. По приглашению американского математика Гана Тяня (Gang Tian) Перельман приехал в Соединенные Штаты и провел лекционный тур. Он выступал, в частности, в Массачусетском технологическом институте (где его слушал и Джордан Элленберг) и в Принстоне, где его слушали многие ведущие математики, например автор доказательства теоремы Ферма Эндрю Уайлс (Andrew Wiles) и нобелевский лауреат Джон Форбс Нэш-младший (John Forbes Nash, Jr.), известный российскому зрителю по фильму "Игры разума". Казалось, все развивается нормально. Перельман рассказывал о ключевых моментах доказательства и отвечал на многочисленные вопросы.
18 апреля 2003 года работающий в США китайский математик, лауреат Филдсовской премии Яу Шинтун (Shing-Tung Yau) опубликовал в Science заметку, в которой заявил, что Перельман, может быть, что-то и доказал, но его доказательство настолько конспективно, что непонятно, доказательство ли это вообще. Яу писал, что очень многие попытки доказать гипотезу Пуанкаре спотыкались как раз на пропущенных казавшихся очевидными деталях. В конечном счете Яу оценил работу Перельмана так: "Это не математика, это — религия". Яу Шинтун вместе с американским математиком Ричардом Гамильтоном (Richard Hamilton) много лет занимался гипотезой Пуанкаре. А Перельман учился у Гамильтона в 1993 году. Гамильтон фактически поставил задачу, с которой сам не справился — с ней справился Перельман.
17 июля 2003 года Перельман опубликовал последнюю — третью — часть доказательства. Теперь уже было что всерьез проверять. Что совсем необычно, Перельман ограничился публикацией на arXiv.org и даже не попытался опубликовать свою работу в реферируемом журнале. Математики Ган Тянь и Джон Морган (John Morgan) при поддержке Математического института Клэя начали планомерную проверку доказательства Перельмана.
10 сентября 2004 года Перельман получил письмо от Тяня: «It is all right». Но Перельман даже не ответил.
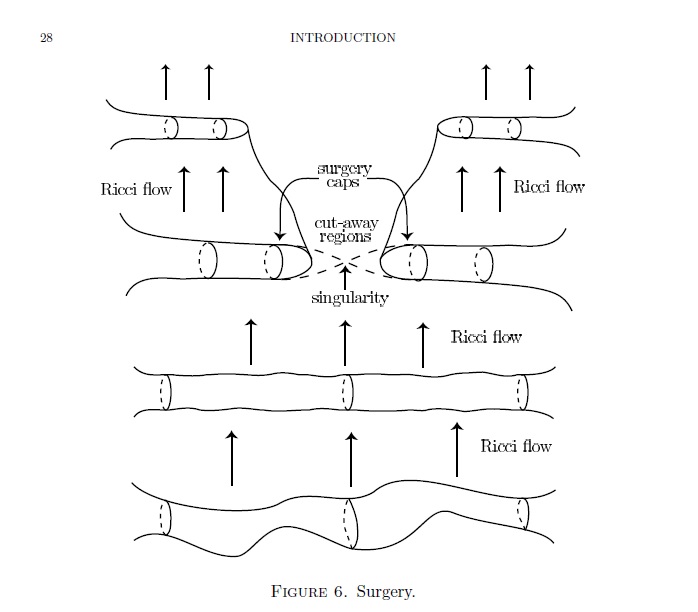
13 апреля 2006 года в редакцию Asian Journal of Mathematics пришло письмо Яу, в котором он сообщал, что посылает статью своих учеников, тоже известных математиков, посвященную «детальному и строгому доказательству гипотезы Пуанкаре». Статья была опубликована в кратчайшие сроки и заняла целый том журнала — триста страниц.
3 июня 2006 года Яу собрал пресс-конференцию в математическом институте в Пекине, где заявил, что в решение проблемы Пуанкаре сделали вклад несколько ученых: 50% — Гамильтон, 25% — Перельман и 30% — китайские математики. Яу не обратил внимания на такую мелочь, как сумма этих процентов: она оказалась больше ста.
20 июня 2006 года на конференции по теории струн в гостинице «Дружба» в Пекине Яу прочел лекцию о гипотезе Пуанкаре. В своем выступлении он отметил и вклад Перельмана в ее решение. Но сказал, что Перельман, безусловно, нашел несколько ключевых моментов, но не изложил доказательство детально, а вот китайские товарищи все разложили по полочкам и уж у них-то все строго. Когда Яу закончил, никто не задал ему ни одного вопроса.
22 августа 2006 года в Мадриде открылся Международный математический конгресс, на котором, в частности, было объявлено, что Филдсовская медаль присуждается Григорию Перельману за доказательство гипотезы Пуанкаре. Достижения китайских математиков в этой области оценены не были. Перельман в борьбе за свой приоритет никакого участия не принимал. Это сделали другие ученые, и надо отдать должное математическому сообществу — оно было солидарно в поддержке приоритета российского математика. Перельман на конгресс не приехал и от Филдсовской медали отказался.
28 августа 2006 года The New Yorker опубликовал статью Сильвии Назар и Дэвида Грубера "Многообразие судьбы" ("Manifold Destiny". A legendary problem and the battle over who solved it.) Авторы статьи – последние на сегодняшний день журналисты, с которыми говорил Григорий Перельман. Русский математик, живущий в Париже, лауреат Абелевской премии Михаил Громов сказал корреспондентам журнала The New Yorker, что понимает Перельмана: "Для великой работы нужен ясный ум. Вы можете думать только о математике. Все остальное — человеческая слабость. Принять премию — продемонстрировать свою слабость. Идеальный ученый делает науку и больше ни о чем не заботится. Перельман хочет жить идеально. Не думаю, что это ему целиком удается. Но он хочет этого".

22 декабря 2006 года журнал Science назвал доказательство гипотезы Пуанкаре научным прорывом года.
18 марта 2010 года Институт Клэя объявил о присуждении Перельману премии тысячелетия.
Согласно положению о премии, после первоначальной проверки решения и его публикации должно пройти два года, чтобы математическое сообщество могло спокойно поискать ошибки и сжиться с мыслью о том, что гипотеза стала теоремой. Институт Клэя колебался четыре года.
В нарушение положения о премии доказательство Перельмана не было опубликовано в рецензируемом авторитетном журнале, а выложено на сайте arXiv.org Зато была опубликована книга с подробной проверкой доказательства (John Morgan, Gang Tian. Ricci Flow and the Poincare Conjecture. American Mathematical Society. Clay Mathematical Institute. Clay Mathematics Monographs. Vol. 3, 2007) и математическое сообщества было убеждено, что доказательство Перельмана верно и приоритет принадлежит именно ему. Тем не менее Математический институт Клэя оказался в трудной ситуации.
С одной стороны премию необходимо было вручить. Поскольку ни разу не врученная премия существует как бы только в проекте. И совершенно неизвестно сколько лет ждать решения следующей "проблемы тысячелетия": выбраны такие задачи, что, вполне возможно, ни одна из них и не будет решена не только в ближайшие годы, но и десятилетия.
С другой стороны была высока вероятность, что Перельман от премии откажется, а это на репутации премии отразится негативно. Тем более сама идея премии - огромные награды, назначенные за решение пусть и важных, но всего 7 задач, к которым математика заведомо не сводится, эта идея в математическом сообществе приветствовалась далеко не всеми.
Российский математик Анатолий Вершик в 2006 году в связи с присуждением Перельману Филдсовской медали и возможности присуждения премии тысячелетия опубликовал статью “Что полезно математике? Размышления о премиях Clay Millenium", в которой он пишет: "На мой взгляд, весь этот ажиотаж и суета свидетельствуют о том, что подобный способ пропаганды математики ущербен и неприемлем, он не популяризирует науку, а, наоборот, вызывает у людей недоумение или нездоровый интерес. И я не думаю, что эти страсти объясняются только особенностями поведения сегодняшнего героя, которые, конечно, несколько обостряют эти эмоции; дело глубже. Вопрос в том, нужен ли математике такой площадный интерес?.. Объяснение состоит в том, что слишком тесно увязаны мало совместимые вещи — серьезный научный результат и вылезающий на первый план "миллион"".
Также Вершик отмечает: "Есть и другие, явно непредусмотренные, последствия этой "миллионной" затеи. Вот одно из них. Как показывает нынешний пример, у некоторых вполне серьезных математиков появляется соблазн затеять дискуссию о приоритете, используя существующие и не существующие шероховатости. Это делается профессионально, но трудно отделаться от мысли о том, что цель этих действий не только разделить почет решения трудной задачи, но и награду". Ясно, что Вершик имеет ввиду Яу и других китайских товарищей.
1 июля 2010 года Перельман публично заявил о своем отказе от премии: "Я отказался. Вы знаете, у меня было очень много причин и в ту, и в другую сторону. Поэтому я так долго решал. Если говорить совсем коротко, то главная причина — это несогласие с организованным математическим сообществом. Мне не нравятся их решения, я считаю их несправедливыми. Я считаю, что вклад в решение этой задачи американского математика Гамильтона ничуть не меньше, чем мой". (Википедия дает ссылку на Интерфакс, но страница Интерфакса недоступна)
Отказ Перельмана стал сильным аргументом в пользу математиков, критиковавших премию Института Клэя.
Миллион, от которого отказался Перельман, Институт Клэя использовал, видимо, оптимально: совместно с Институтом Анри Пуанкаре в Париже (the Institut Henri Poincaré - IHP, Paris) была создана специальная позиция (Poincaré Chair) для молодых и многообещающих математиков. Ее занимают от полугода до года. Позиция финансируется из фонда, образованного премией непринятой Перельманом. Позиция была открыта в 2010 году после объявления о присуждении премии за доказательство гипотезы Пуанкаре и рассчитана на пять лет.
В 2011 году Ричарду Гамильтону и Деметриосу Кристодулу была присуждена Премия Шао по математике в размере миллион долларов. Ричард Гамильтон был награжден за создание математической теории, которую затем развил Григорий Перельман в своих работах по доказательству гипотезы Пуанкаре. Гамильтон премию принял.
В 2014 году появились сообщения, что Перельман переехал на постоянное место жительства в Швецию.
Маша Гессен о Перельмане
Сразу после отказа от Филдсовской медали Перельман стал сенсацией. Маша Гессен написала о Перельмане книгу.

Masha Gessen. Perfect Rigor. A Genius and the Mathematical Breakthrough of the Century. Boston — New York, «Houghton Mifflin Harcourt», 2009, 242 стр.
Маша Гессен. Совершенная строгость. Григорий Перельман: гений и задача тысячелетия. Перевод с английского И. Кригер. М., «Астрель», «CORPUS», 2011, 272 стр.
Книга Маши Гессен сначала вышла на английском языке и только спустя два года была переведена на русский. Гессен не удалось поговорить с героем своей книги Григорием Перельманом, но она поговорила о нем с очень многими людьми, хорошо знавшими Перельмана и принимавшими в его судьбе самое деятельное участие. Это в первую очередь — руководитель математического кружка, в котором занимался Перельман, будучи школьником, — Сергей Рукшин. Рассказ Рукшина о Перельмане очень любопытен. Если верить Рукшину, Перельман был юношей, сосредоточенным до жестокости, — и к себе и к другим. Он не понимал и не принимал ни малейшей расслабленности. В определенном смысле Перельман структурировал внешний — неизбежно хаотичный — мир по законам математики и не терпел ошибок и отклоненй. И этот образ гениального математика проходит через всю книгу.
Естественно, что все читатели этой книги искали в ней ответ на сакраментальный вопрос: почему Перельман, добившись выдающегося успеха — доказав проблему Пуанкаре, — повел себя настолько неадекватно: отказался сначала от Филдсовской медали, потом — от премии Института Клэя и наконец вовсе ушел из математики? У Гессен есть такой ответ: Перельман страдает синдромом Аспергера — формой аутизма, при которой у человека затруднены коммуникации с внешним миром. В частности, такой человек просто не может поставить себя на место другого, а это необходимо для нормального взаимопонимания. Вот это нарушение социализации и привело к таким неадекватным реакциям. Насколько этот ответ правильный, судить трудно, поскольку для этого необходимо, чтобы Перельмана обследовали врачи. А это вряд ли возможно.
Что-то верное в таком ответе, видимо, есть. Наталья Берлова, заведующая кафедрой квантовых жидкостей факультета прикладной математики и теоретической физики Кембриджского университета, рассказала в своем интервью: "Наш факультет, из-за того что мы мало принимаем женщин, постоянно ругают на всех университетских комитетах: почему и как же так? Но уже лениво, потому что из года в год повторяется, что у нас только десять процентов всех студентов — женщины. Старший тьютор, ответственный за прием, из года в год оправдывался. Наступил последний, десятый год его пребывания в должности, и на последнем для него собрании в этой должности он встал и вдруг сказал: "Ну как вы не поймете, чтобы быть талантливым математиком, надо быть практически аутистом. А это мужская особенность". И никто не нашелся что возразить". То есть это довольно типичная ситуация.
Книгу Гессен можно условно разделить на две на самом-то деле не слишком связанные темы: одна — это Григорий Перельман, его биография, его поведение, встречи и разговоры с другими математиками. И здесь все в порядке — это хорошая журналистская работа. Но есть и вторая тема — это сама проблема Пуанкаре. Здесь все гораздо хуже.
Когда мне случилось готовить к публикации в "Новом мире" работу Владимира Успенского "Апология математики" - это было довольно мучительно. Владимир Андреевич, объясняя свою строгость в подготовке текста, сказал: "Володя, если бы я готовил эту публикацию для математического журнала, я бы так не беспокоился — там, заметив ошибку или опечатку, профессионал все равно прочел бы текст правильно. Когда мы готовим популярный текст, адресованный непрофессионалам, мы должны быть предельно внимательны, поскольку большинство наших читателей примут все, что сказано, на веру".
Математики относятся к тем немногим людям на Земле, которые, что называется, "отвечают за базар". Отвечают если не собственной жизнью, то собственной репутацией и карьерой, то есть в конечном счете возможностью продолжать нормально заниматься делом своей жизни. Грубая ошибка может привести к реальному остракизму, что для математика сравнимо едва ли не с потерей жизни и свободы. Просто потому, что разговаривать о вещах, которые его больше всего на свете интересуют, ему попросту не с кем, кроме других математиков. С человеком, солгавшим или даже допустившем ошибку и упорствующем в своем заблуждении, никто говорить не станет.
Математик, взявшийся популяризировать свою науку, многократно рискует. Коллеги все равно будут разочарованы, поскольку у каждого свое представление о допустимом уровне профанации. Это — с одной стороны. С другой — математик представляет свой неведомый континент тем, кто никогда там не был и скорее всего никогда туда не попадет. Как он скажет, так и будет. Скажет, что там живут люди с песьими головами, — значит, так и есть, проверить это почти невозможно — для человека, не получившего математического образования, это годы труда.
Слово в математике значит то и только то, что оно значит. Поэтому обращаться с ним нужно крайне аккуратно. Изъятое из контекста, оно часто просто теряет смысл, и поэтому, насколько это возможно, его следует охранять от произвольных интерпретаций и контекстов.
Гессен тоже говорит о строгости и специфичности языка математики, но сама делает такие ошибки, что просто опускаются руки. Приведу несколько примеров. "Картина мира по Евклиду была ограниченной и плоской. Наш мир искривлен. Современные люди легко покрывают расстояния достаточно большие для того, чтобы почувствовать на себе кривизну Земли". Кривизна пространства-времени, о которой писал Эйнштейн (и которую имеет в виду Гессен), не имеет никакого отношения к "кривизне Земли", которую может наблюдать обычный человек. Сфера прекрасно вкладывается в "ограниченный и плоский" Евклидов мир. Или Гессен считает, что греки не знали, что такое шар? Я что-то сомневаюсь сильно. "Ситуация меняется, если в сфере появляется отверстие. Тогда сфера перестает быть сферой и становится тором…". Нет, не становится. Сфера с дыркой гомеоморфна плоскости, а не тору.
Но надо отметить, что в английском тексте ошибок все-таки меньше, чем в русском переводе. К тем неточностям и ошибкам, которые есть в английском тексте, переводчик щедро добавляет свои — часто он просто не понимает, о чем идет речь. Вот чисто переводческий ляп. Название статьи Сильвии Назар и Дэвида Грубера, посвященной Григорию Перельману, - "Manifold Destiny". В английском тексте книги Гессен, естественно, все в порядке, а на русский название переведено: "Многоликая судьба". Это никуда не годится. "Manifold" — это в том числе и математический термин, который переводится на русский математическим же термином — "многообразие". Этими самыми "многообразиями" как раз и занимается топология, и о них идет речь в проблеме Пуанкаре. Название статьи построено на игре слов. И эту игру очень просто перевести на русский: "Многообразие судьбы". Откуда взялась эта «многоликость»? Я подозреваю, что переводчик просто не знал, что "manifold" — математический термин. Но я не понимаю, почему его не поправил автор.
Приведу еще один пример. Гессен пишет, что семилетний Андрюша Колмогоров придумал такую задачу. В пуговице четыре дырки. Пуговица считается пришитой, если есть хотя бы один стежок. Сколько существует разных способов пришить пуговицу? (Ученик Колмогорова Владимир Тихомиров уточнил со слов Колмогорова, что в задаче требовалось, чтобы все дырки были задействованы. Тогда решение будет другим, но мы займемся задачей, которую сформулировала Маша Гессен)
Гессен пишет: "Попробуйте на досуге сами ответить на этот вопрос. Я знаю двух профессиональных математиков – оба, кстати, ученики Колмогорова, - которые пришли к двум различным мнениям". У этой задачи есть решение - существует в точности 63 варианта пришить пуговицу.
Гессен пишет, что математики "пришли … к двум разным мнениям". Но в математике не бывает "мнений", там либо есть решение, либо его нет.
Гессен давит на читателя, его дезориентирует, ссылаясь на непререкаемые авторитеты – математиков, учеников Колмогорова (жаль только не приводит фамилии). Такие трюки проходят в любой идеологизированной сфере, но в математике не проходят. Мы просто делаем вывод: Гессен не справилась с элементарной задачей, с которой справится школьник. Шестиклассникам на Олимпиадах дают задачи несравнимо сложнее.
Многие ошибки в книге Гессен легко устранить, но вместо того, чтобы сделать это, например, в русском переводе, к уже существующим в английском тексте добавились новые. Ошибки подрывают доверие к тексту, и даже то, что в нем интересно, вызывает неизбежные сомнения. И ни о какой "совершенной строгости" речь, конечно, идти не может.
Слезы “Комсомолки”
После отказа от миллиона Перельман стал первополосным героем. Буквально поп-звездой. И “Комсомольская правда” не осталась в стороне… В апреле 2011 года газета опубликовала “интервью с Перельманом", спустя пять лет после его последнего развернутого публичного высказывания.
Это интервью сразу вызвало серьезные сомнения в его подлинности. И я решил его проверить “на всхожесть”.
Мог ли всемирно известный математик сказать то, что ему приписывает газета? Я попробую подробно прокомментировать статью «Комсомолки» - «Интервью с математиком Григорием Перельманом: Зачем мне миллион долларов? Я могу управлять Вселенной» и представить себе насколько вообще реально, что эти слова принадлежат математику. Причем анализировать я буду только высказывания, приписанные Григорию Перельману. (Грубые ошибки есть в авторском тексте статьи, но их я касаться не буду, просто потому что ошибки в статьях «Комсомолки» и прочей «желтой» прессы событие рядовое и никого удивить не могут.)
Я приведу интервью с «Григорием Перельманом» почти полностью и его последовательно прокомментирую. Вопросы - выделены курсивом, ответы «Перельмана» даны прямым шрифтом.
Текст
- Григорий Яковлевич, еще школьником вы представляли СССР на математической олимпиаде в Будапеште. И взяли золотую медаль…
- Готовясь к олимпиаде, мы пытались решать задачи, где непременным условием было умение абстрактно мыслить. В этом отвлечении от математической логики и был главный смысл ежедневных тренировок. Чтобы найти правильное решение, необходимо было представить себе «кусочек мира».
Комментарий. Что здесь сказано? Чтобы решать задачи нужно умение абстрактно мыслить? Ну в целом верно, главное - ново. Только вот почему «умение абстрактно мыслить» требует отвлечения от «математической логики»? Математическая логика – одна из областей математики, которая как раз и посвящена вопросу, как возможно математическое мышление - «умение абстрактно мыслить». Отвлекать школьников от математической логики нет никакой необходимости, поскольку они ее не знают – с этим предметом студенты сталкиваются уже в университете, и то, если они не специализируются в этой области, то только чуть-чуть по касательной – сдали-забыли. Знание математической логики не требуется, ни для того чтобы решать олимпиадные задачи, ни для того чтобы подготовиться к поступлению в университет. Олимпиадные задачи требуют знания элементарной математики, а это довольно специальная область, которую и изучают в школе. Несмотря на название, «элементарная математика» отнюдь не элементарна, а задачи, которые решают на международных школьных олимпиадах, всегда крайне сложны. Они требуют изощренных навыков, умения быстро думать и не в последнюю очередь готовности к борьбе за победу и психологической устойчивости. А математическая логика во-первых здесь просто не причем, а во-вторых еще никому не помешала решать задачи.
Текст.
- А не припомните ли какую-нибудь задачу той поры, казавшуюся неразрешимой?
- Неразрешимой… Пожалуй, нет. Труднорешаемой. Так точнее. Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху. Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться.
Комментарий. Понятие «неразрешимая задача» имеет строгое математическое определение и с «труднорешаемой задачей» оно никак не связано. Примером труднорешаемых (но в принципе разрешимых) задач являются, например, Великая теорема Ферма или проблема Пуанкаре. Обе эти задачи очень сложны, но разрешимы и, как мы знаем, уже решены. Примером неразрешимой задачи является, например, «квадратура круга»: «С помощью циркуля и линейки построить квадрат по площади равный данному кругу». Эту задачу нельзя решить, и строгое доказательство ее неразрешимости получено в XIX веке. Между «неразрешимыми» и «труднорешаемыми» задачами лежит пропасть. Человек говорящий «Неразрешимой… Пожалуй, нет. Труднорешаемой. Так точнее» очевидно этого не понимает. Задача о том «с какой скоростью нужно идти по воде, чтобы не провалиться» давно и хорошо известна. Например, Петр Капица предлагал ее студентам Физтеха в качестве темы для исследования еще в 40-ые годы. Ни на каком математическом кружке, ни на какой математической олимпиаде такую задачу предложить не могли. Отбор олимпиадных задач происходит по нескольким неукоснительным принципам: 1) задача должна быть новой, то есть впервые опубликованной прямо во время олимпиады, иначе соревнующиеся могут оказаться в неравных условиях – тот кто знает задачу, просто запишет решение 2) на математической олимпиаде все задачи по математике, а не по физике или по химии (что вообще-то довольно естественно) 3) для решения задачи должно хватать знания элементарной математики. Задача о «хождении по водам» не отвечает ни одному из этих требований: она широко известна, это задача по физике – более точно по гидродинамике, она требует понимания таких явлений как вязкое трение, а в школе его не изучают. (Возможно, вам случалось видеть, как играют в водное поло. Там игроки и особенно вратари умеют подниматься из воды – по пояс. Они именно "стоят" на воде, используя вязкое трение.)
Текст.
- А вы знаете, что мне пришлось поломать голову, выбирая профессию?
- Как же так?
- Я имел право без экзаменов поступать в любое учебное заведение Советского Союза. Вот и колебался между мехматом и консерваторией. Выбрал математику… Мне сейчас очень интересно вспоминать студенческие годы. Мы так много успевали тогда… Процесс познания захватывал… Мы забывали о днях недели и времени года.
Комментарий. Перельман поступил в Ленинградский университет в 1982 году. Участники международных олимпиад, действительно имели право поступать в любой институт или университет Советского Союза без вступительных испытаний. Но как правило, участники международной олимпиады специальность не выбирают, по очень простой причине: они ее давно выбрали. Иначе они бы никогда не попали в международную команду. Это – одаренные люди, потратившие годы труда на решение задач. Но сколько бы ты не потратил времени и сил, если нет таланта – у тебя все равно ничего не получится. Их труд и талант посвящены одной цели – изучению математики. Можно себе представить гипотетическую ситуацию. Допустим, ежегодно проводится международный музыкальный конкурс для школьников, наподобие конкурса Чайковского. И участники этого конкурса получают право поступать без экзаменов в любое высшее учебное заведение. Неужели они пойдут на мехмат? А как же огромный труд, который потрачен и несомненный талант, который уже проявлен? Похоронить? И ведь нельзя же не понимать, что поступить одно, но ведь надо еще и учиться, и потом профессионально заниматься выбранным родом деятельности. А это просто невозможно. Уж если ты математик, вряд ли ты великий скрипач, и наоборот. Участники международных олимпиад по математике поступали на ведущие математические факультеты Советского Союза. Чаще всего на мехмат МГУ или на питерский матмех, иногда на Новосибирский мехмат. Редко на Физтех, совсем редко в другие ведущие вузы, но тоже на математические специальности. Человек говорит: «Я колебался между мехматом и консерваторией». Поколебался-поколебался между мехматом и консерваторией, а потом поступил на матмех. Никогда ни один студент питерского матмеха не назовет свой факультет мехматом (как и наоборот). Мехмат – это в Москве, и между этими факультетами существует серьезная конкуренция.
Текст.
- В двадцать с небольшим лет вы сказали новое слово в науке...
- Никаких слов я не говорил… Просто продолжал исследовать проблемы изучения свойств трехмерного пространства Вселенной. Это очень интересно.
Комментарий. Фраза "исследовать проблемы изучения свойств" крайне загадочна. Просто непонятно, что собственно "исследовать"? Но дело гораздо хуже: Вселенная не трехмерна. Такую ошибку не может сделать даже школьник, который уже слышал, что пространство Минковского, которое описывает теория относительности – четырехмерно. А теория струн склоняется к тому, что измерений еще больше. Может быть, 10. Но никак не 3.
Текст.
- Пытались объять необъятное?
- Совершенно верно… Только ведь любое необъятное тоже объятно. Диссертацию писал под руководством академика Александрова. Тема была несложной: «Седловидные поверхности в евклидовой геометрии». Можете представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности? Нам нужно измерить «впадины» между ними.
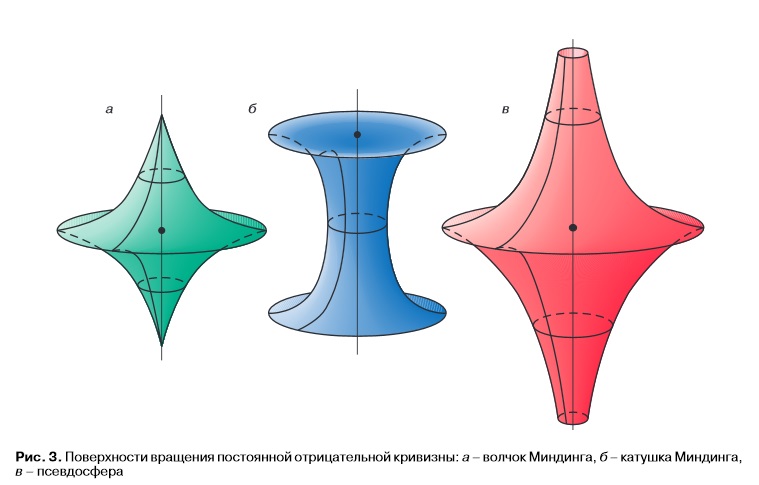
Комментарий. Диссертация Перельмана носит название: «Седловые поверхности в евклидовых пространствах». Вероятно, отвечающий на вопросы запамятовал название собственной диссертации. Все остальное не имеет смысла: «представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности» - нельзя, а уж «впадины между ними измерить», тем более. И чем «измерить»-то? Линейкой что ли? (О седловых поверхностях см. Фоменко В.Т., Поверхности отрицательной кривизны. — Соросовский образовательный журнал, N 12, 1999)
Текст.
- Это теория?
- Это уже практика. По какой орбите полетит космический корабль к созвездию Псов? Какие препятствия встретит на своем пути… Хотите еще проще? Стоит ли косить сено между тремя холмами? Сколько людей и машин для этого надо? Министерство сельского хозяйства, оказывается, ни к чему. Есть формула. Пользуйся. Считай. И никакие кризисы тебе не страшны.
Комментарий. «Есть формула». Формула чего? Холмов? Впадин? Людей? Машин? Наверное, министерства сельского хозяйства. Но с "препятствиями" при полете "к созвездию Псов" дело совсем плохо. Препятствия эти непреодолимы, потому что лететь-то собственно некуда. Любое созвездие, это не физический объект к которому можно было бы лететь, а виртуальный – это проекция звезд, галактик, звездных скоплений на небесную сферу. Когда мы смотрим на небо, нам кажется, что они рядом, но ведь между ними на самом-то деле огромные расстояния. Альфа созвездия Гончих Псов (никакого «созвездия Псов» - нет) – звезда Сердце Карла находится на расстоянии примерно 100 световых лет от Земли, а вот галактика M51, которая видна как одна из звезд созвездия, находится на расстоянии более 37 миллионов световых лет от Земли. Так куда летим?
Текст.
- А не схоластика ли это?
- Это колесо, топор, молот, наковальня - все что угодно, но только не схоластика. Давайте разберемся. Особенности современной математики заключаются в том, что она изучает искусственно изобретенные объекты. Нет в природе многомерных пространств, нет групп, полей и колец, свойства которых усиленно изучают математики. И если в технике постоянно создаются новые аппараты, всевозможные устройства, то и в математике создаются их аналоги - логические приемы для аналитиков в любой области науки. И всякая математическая теория, если она строгая, рано или поздно находит применение. К примеру, многие поколения математиков и философов пытались аксиоматизировать философию. В результате этих попыток была создана теория булевых функций, названных по имени ирландского математика и философа Джорджа Буля. Эта теория стала ядром кибернетики и общей теории управления, которые вместе с достижениями других наук привели к созданию компьютеров, современных морских, воздушных и космических кораблей. Таких примеров история математики дает десятки.
Комментарий. "Нет в природе многомерных пространств, нет групп, полей и колец, свойства которых усиленно изучают математики". Ну отчего же нет? По крайней мере, одно пространство точно есть – поглядите вокруг, и оно многомерно, согласно теории относительности четырехмерно. И поля, и кольца, и группы – все это, конечно, есть в природе. В наших повседневных расчетах мы обычно оперируем действительными числами, а они как раз образуют поле. А скажем, группа Лоренца работает в теории относительности, а эта теория описывает именно то пространство, в котором мы живем. Джордж Буль – не ирландский математик, а английский. Он действительно один из создателей теории булевых функций (или более строго «функций алгебры логики»). Алгебра логики действительно имеет самое непосредственное отношение к созданию вычислительных машин, но она не имеет отношения к теории управления. Кибернетика – это описанная Норбертом Винером в 40-ые годы междисциплинарная область исследований, посвященная общим задачам управления. Но как самостоятельная наука она уже давно не существует (да и непонятно существовала ли), и к созданию компьютеров не имеет никакого отношения.
Текст.
- Значит, каждая ваша теоретическая разработка имеет прикладное значение?
- Безусловно. Для чего столько лет нужно было биться над доказательством гипотезы Пуанкаре? Попросту суть ее можно изложить так: если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу. «Формулой Вселенной» утверждение Пуанкаре называют из-за его важности в изучении сложных физических процессов в теории мироздания и из-за того, что оно дает ответ на вопрос о форме Вселенной. Сыграет это доказательство большую роль в развитии нанотехнологий.
Комментарий. Чтобы "попросту изложить" именно формулировку, а никак не доказательство проблемы Пуанкаре, Владимиру Успенскому, доктору физико-математических наук, заведующему кафедрой логики и теории алгоритмов мехмата МГУ им. М.В. Ломоносова, потребовалось много десятков страниц довольно непростого текста. Успенский поставил перед собой именно такую задачу: «попросту» объяснить суть дела для гуманитариев. На мой взгляд, в его замечательной книге "Апология математики" формулировка проблемы Пуанкаре - это самое трудное место. И боюсь, что полностью разобраться в этом предельно простом (проще без потерь и искажений нельзя), но корректном изложении проблемы Пуанкаре может, увы, только человек, получивший математическое образование. Приведенное высказывание "если трехмерная поверхность в чем-то похожа на сферу, то ее можно расправить в сферу" - это грубый журналистский штамп, который немыслим в устах математика. А Перельман собственно уже один раз сформулировал и саму проблему и ее доказательство. Читайте его работы, если интересно, если сможете. "Формулой Вселенной" утверждение Пуанкаре опять-таки называют только ничего непонимающие в этом утверждении журналисты. Нету никакой формулы Вселенной. Просто нету. «Сыграет это доказательство большую роль в развитии нанотехнологий». Эта фраза меня окончательно добила. В огороде бузина, но и она сыграет большую роль в развитии нанотехнологий.
Текст.
- Значит, «бодрые» «жизнеутверждающие» доклады «пионеров» этой отрасли…
- Абсолютная чепуха и бессмыслица. Попытка построить дом на песке… Я научился вычислять пустоты, вместе с моими коллегами мы познаем механизмы заполнения социальных и экономических «пустот». Пустоты есть везде. Их можно вычислять, и это дает большие возможности… Я знаю, как управлять Вселенной. И скажите - зачем же мне бежать за миллионом?!
Комментарий. Да, действительно с этим можно только согласиться – абсолютная чепуха, бессмыслица и вычисление пустот. Безо всяких кавычек. Да и "бежать за миллионом" никуда не надо было, надо было просто согласиться его принять.
Можно сделать некоторые выводы. Человек, отвечающий на вопросы:
- никогда не участвовал в математических олимпиадах,
- никогда не учился на матмехе,
- не помнит, как называлась кандидатская диссертация Григория Перельмана,
- не знает, что такое «неразрешимая задача»,
- не знает, что такое седловые поверхности,
- не знает, что такое созвездия,
- не знает, что окружающее нас пространство не трехмерно,
- не знает, как связаны алгебра логики, кибернетика, компьютеры и теория управления.
Он не понимает "Для чего столько лет нужно было биться над доказательством гипотезы Пуанкаре?", если результат не имеет прикладного значения, то есть не представляет себе ни работы математиков, ни их целей, ни их ценностей. Кроме того, он очень озабочен пропагандой своих результатов и готов их излагать на недопустимо низком уровне строгости, то есть попросту неверно. Ну и нанотехнологии его очень волнуют.
Этот человек говорит банальности. Одни банальности, иногда пуская пыль в глаза – "в бесконечности равновеликие и неравномерно удаленные". Информативность этого эксклюзивного интервью – близка к нулю. Этому человеку просто нечего сказать. И это не удивительно – он почти ничего не знает.
И этот человек Григорий Перельман?! Я в это поверить не могу. И хотя все приведенные мной доказательства того, что человек, отвечающий на вопросы в этом интервью, не имеет к Григорию Перельману никакого отношения, только косвенные, для меня их достаточно.
Этот человек не владеет даже знаниями прилежного старшеклассника. Это – жизнерадостный открытый миру дилетант-недоучка, который и соврет недорого возьмет.
А мы говорим об одном из крупнейших математиков нашего (а может быть, и не только нашего) времени, о человеке предельной научной честности.
Но вот что любопытно: я не могу представить себе другого человека чье поддельное интервью, грубо слепленное из каких-то обрывков случайных сведений, вызвало бы такой мощный резонанс. Фактически Перельман уже стал героем собственного мифа. И он действительно привлек общественное внимание к работе математиков. И многие молодые люди могут всерьез задуматься: а чем в действительности они там занимаются? Получить ответ будет трудно. Но тот, кто войдет в этот волшебный сад, как называл математику Давид Гильберт, будет вознагражден. И не миллионом долларов, а чем-то куда большим.
Однажды Редьярд Киплинг, предостерегая студентов от чрезмерной зацикленности на деньгах, власти или славе, сказал: "Однажды вы повстречаете человека, для которого все это не имеет значения. И тогда вы поймете, как вы бедны". Кажется, Григорий Перельман заставил целый мир задуматься над этой старой простой истиной.
Сильнее, чем миллион

Перельман отказался принять не только миллион, но и внешние знаки славы - почетные доктораты, членство в академиях, публичные лекции, участие в приемах, интервью и т.д.. И его слава стала запредельной. Если бы он поставил перед собой задачу стать максимально известным, то лучшей стратегии поведения он просто не смог бы придумать. Именно отказ принимать почести и премии сделал его самым знаменитым математиком в мире и вообще одним из самых знаменитых наших современников. Есть такой тест: назовите первую ассоциацию со словом. Фрукт — яблоко. Поэт — Пушкин. Математик — сегодня и надолго — это Перельман. Слава Эндрю Уайлса, доказавшего куда более знаменитую проблему – великую теорему Ферма, с известностью Перельмана просто несравнима. Да и Пуанкаре известен сегодня широкой публике только в связи с Перельманом. То, что публика заговорила о Перельмане только тогда, когда запахло миллионом долларов, — это естественно и нормально. Почти никто не знает, что он там доказал, и зачем это нужно было доказывать, и даже что такое "доказательство". А про миллион — тут все понятно. Отказался — значит идиот. Но ведь ему же этот миллион дают, потому что он самый умный. Что-то не вяжется. Ситуация парадоксальная.
И до сих пор поступок Перельмана не дает покоя нормальным людям.
Гессен объяснила отказ Перельмана от премии психическим расстройством.
”Комсомолка" попыталась объяснить - желанием неограниченной власти.
Я тоже придумал свое объяснение - в виде пьесы о гениальном математике - “Гипотеза о душе”.
На самом деле Перельман еще вполне может вернуться к активной научной работе. Ему 49 лет. Когда Джон Форбс Нэш-младший серьезно заболел ему был 31 год. И он надолго фактически ушел из математики. Но потом - вернулся. Нэш называл этот период своей жизни - “каникулы в 25 лет”.
Статья Джордана Элленберга, из которой я когда-то узнал о Перельмане, посвящена вообще-то не только гипотезе Пуанкаре. Элленберг задается вопросом: правда ли, что математик может активно работать только до 30 лет? И отвечает: нет, это – миф: "…когда Пуанкаре сформулировал свою гипотезу. Ему было 50 лет".
Всему человечеству было бы спокойнее жить, если бы Перельман получил этот миллион. Или на худой конец занял миллионную позицию в MIT или в Принстоне. А он - отказывается. Что-то он такое знает, что-то такое у него есть, о чем большинство народонаселения может только смутно догадываться. Может быть, это – любовь к истине? А поиск истины сам по себе величайшая награда?
Миллион, конечно, сила, но Перельман оказался сильнее.







 Сергей Беляков. О «Генеральном плане Ост»
Сергей Беляков. О «Генеральном плане Ост» Виктор Белкин. Гора и Рэм. (Фортамбек 1977 год)
Виктор Белкин. Гора и Рэм. (Фортамбек 1977 год) 8 июня Александр Лазарев
8 июня Александр Лазарев
