
Выбор редакции
Проекты
Как не надо преподавать математику философам

Хочу поговорить о преподавании математики студентам философских факультетов. В качестве кейса я буду использовать преподавание математики на первом курсе философского факультета Вышки (НИУ ВШЭ), поскольку (так уж случилось) знаю этот кейс довольно детально.
Во-первых, на мой взгляд, выбранный в Вышке подход мало что дает будущему философу кроме головной боли и галочки в зачетке (или что там у них теперь вместо нее?). Во-вторых, преподавать математику философам и можно, и нужно, но исходить необходимо из других соображений (о них ниже). И наконец, третье, преподавание математики должно идти в тесной связке – с логикой, естествознанием и – самое главное – с философией, и сам предмет желательно строить на основе некоторой философской (может быть, даже историко-философской) парадигмы, а не на традиционной схеме, основой которой является математический анализ и тренировка в решении задач.
Программа курса математики для философов, читаемого в Вышке, выложена на сайте университета, с ней можно ознакомиться, и выглядит она при беглом взгляде довольно пристойно.
В целом программа напоминает курс мехмата, и если судить по названиям разделов, не слишком даже урезанный. Все вроде есть – и анализ, и линейка, и теорвер, и теории множеств чуток, и даже логики немножко (у философов есть и отдельный курс логики, о нем я здесь говорить не буду, чтобы не распыляться, хотя и к нему у меня много вопросов). Но есть одна загвоздка: на мехмате этому учат 5 лет (и кроме математики вообще-то ничему не учат), а здесь на всё про всё 54 лекции и 50 семинаров. И кроме того, есть довольно много (для такого краткого курса) экономической математики. В частности, довольно специальной, вроде паутины Вальраса или кривой Лоренца.
На мой взгляд, экономические приложения в курсе для философов – это не совсем то, что нужно. Экономическая математика штука элементарная, если посмотреть на нее, как на набор готовых формул, но и совершенно бесполезная, как любой набор рецептов, предъявленных тому, кто эти рецепты не собирается использовать в жизни. А если заглянуть в экономическую математику более глубоко – она довольно трудная, поскольку имеет дело с теорией игр, дискретными («плохими») функциями и всякими довольно-таки технически изощренными штуками вроде линейного и динамического программирования.
Вот студенту-философу объясняют, что такое интеграл (Римана), учат интегрировать по частям, учат раскладывать рациональные функции на многочлены и простейшие дроби и т.д. Все это, наверно, и полезно было бы, если бы можно было этому научить на паре примеров. Но это невозможно.
Студент мехмата знакомится с интегралом в начале первого курса и больше с интегралом не расстается. Сколько он берет интегралов за время обучения? Тысячи. Сначала считает первообразные, разбирается с интегралом Римана, считает несобственные интегралы, интегралы с параметром, изучает интеграл Лебега, интегралы по кривой, двойные и тройные, узнает теорему Стокса, в теорвере работает с интегралом Лебега-Стильтьеса, в ТФКП с интегралом по контуру, считает вычеты, интегрирует дифференциальные уравнения - и обыкновенные и с частными производными, берет интегралы численно, разбирается с интегральными операторами, с теормехом, с квантовой механикой, где без интегрирования никуда, ну и т. д. В конце концов даже самый нерадивый студент к интегралу привыкает, как к любимой кошке. Через эти бесконечные вычисления, через смену контекстов, через затверженные операционные навыки, через руки - понятие интеграла входит в мозг намертво.
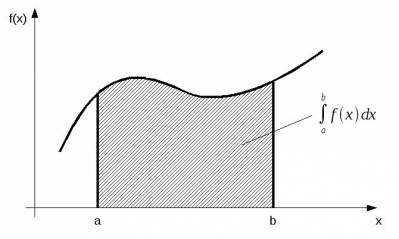 Надо это философу? Видимо, нет. У философа своих проблем выше крыши. Ему надо Платона читать и с Витгенштейном разбираться. Что философу надо? Может быть, ему достаточно знать, что интеграл – это площадь под кривой? Но вот каким таким образом актуально-бесконечная сумма бесконечно-малых дает точный конечный результат, это философ должен понимать. Это его проблема. Вот этому его и надо учить. А показать это, может быть, удобнее даже не на примере интеграла Римана, а на методе исчерпывания Кавальери, на винных бочках Кеплера. То есть надо учить не тому, как считать, например, пределы, а объяснять, почему эпсилон-дельта техника это – строгое рассуждение, а эйлеровы вполне интуитивные построения или ньютоновы флюксии – нестрогое. Как вообще мы, используя конечные логические построения, беремся рассуждать о бесконечном – вот это надо. То есть философу важны не операционные навыки, а демонстрация строгого рассуждения. Именно этот опыт важен. Канторова диагональ должна появляться не в конце курса вскользь едва-едва, а с нее надо вообще-то начинать – с теории множеств. При этом изложение проблемы бесконечного нужно вести от Зенона и Аристотеля, через Плотина, через Кузанского, через диалоги Галилея. Подходить к спору Кантора и Кронекера, к разборкам Гильберта и Брауэра, к размышлениям Кассирера, к теоретико-множественной аксиоматике. Причем не надо здесь тормозить – надо двигаться дальше – к доказательству континуум-гипотезы Геделем и Коэном, и возможно, показать на пальцах (без строгих формулировок и доказательств) метод форсинга - для этого есть отличная именно философская иллюстрация - “Бытие и событие” Бадью. Это совершенно другая дорога к математике, причем к математике современной, а не к математике XVII века - анализу Ньютона и Лейбница.
Надо это философу? Видимо, нет. У философа своих проблем выше крыши. Ему надо Платона читать и с Витгенштейном разбираться. Что философу надо? Может быть, ему достаточно знать, что интеграл – это площадь под кривой? Но вот каким таким образом актуально-бесконечная сумма бесконечно-малых дает точный конечный результат, это философ должен понимать. Это его проблема. Вот этому его и надо учить. А показать это, может быть, удобнее даже не на примере интеграла Римана, а на методе исчерпывания Кавальери, на винных бочках Кеплера. То есть надо учить не тому, как считать, например, пределы, а объяснять, почему эпсилон-дельта техника это – строгое рассуждение, а эйлеровы вполне интуитивные построения или ньютоновы флюксии – нестрогое. Как вообще мы, используя конечные логические построения, беремся рассуждать о бесконечном – вот это надо. То есть философу важны не операционные навыки, а демонстрация строгого рассуждения. Именно этот опыт важен. Канторова диагональ должна появляться не в конце курса вскользь едва-едва, а с нее надо вообще-то начинать – с теории множеств. При этом изложение проблемы бесконечного нужно вести от Зенона и Аристотеля, через Плотина, через Кузанского, через диалоги Галилея. Подходить к спору Кантора и Кронекера, к разборкам Гильберта и Брауэра, к размышлениям Кассирера, к теоретико-множественной аксиоматике. Причем не надо здесь тормозить – надо двигаться дальше – к доказательству континуум-гипотезы Геделем и Коэном, и возможно, показать на пальцах (без строгих формулировок и доказательств) метод форсинга - для этого есть отличная именно философская иллюстрация - “Бытие и событие” Бадью. Это совершенно другая дорога к математике, причем к математике современной, а не к математике XVII века - анализу Ньютона и Лейбница.
И вообще, может быть, основой курса делать не анализ, а топологию. Топологические построения трудно доказывать, но просто показывать – так что этот язык, может быть, для философа более подходящий.
Что может дать математика философу при первом знакомстве? Опыт строгого рассуждения. А здесь едва ли не важнейшее – аксиоматический метод – от Евклида, через неевклидовы геометрии, теорию групп, к современному состоянию дел, возможно, к основным понятиям теории категорий. При этом постоянно опираясь на философскую проблематику математики XX века – формализм и платонизм Гильберта и Бернайса, понятия вычислимости и конструктивности, «физический» подход Арнольда, его спор с Бурбаки и т. д. Не надо бояться сразу давать сложные (с точки зрения математика) понятия – они для философа простые. А элементарные (для математика) вычисления – могут для философа оказаться непреодолимыми. Операционные навыки нужно давать очень аккуратно, и лучше вообще не через интегралы или пределы, а через логические системы. Они сохраняют память о понятии и потому философу гораздо ближе.
А примеры, вероятно, лучше брать не из экономики, а из физики, причем физики XX века – обсуждая теорию эксперимента, понятие измерения, интерпретации квантовой механики, теорию относительности, проблему причинности и т.д. Как все это излагать без формализмов и вообще можно ли об этом рассказать на вполне интуитивном уровне, но без профанации, - это другой вопрос.
И тогда, возможно, кто-то из студентов-философов откроет для себя математику, и выберет философию математики своей специальностью, и тогда ему придется пройти через долгое привыкание к языку и получить те операционные навыки, которые нужны, чтобы математику чувствовать. Но такой студент будет четко понимать, зачем ему нужно умение интегрировать по частям. А у того кто будет специализироваться на других философских предметах, останется опыт строгого рассуждения, которым философ может поверять свои построения, и умение строить формальные модели, которые многое проясняют.
Но я здесь сразу оговорюсь – это только гипотеза. Я философам не преподавал и запросто могу что-то важное не увидеть.






 Сергей Беляков. О «Генеральном плане Ост»
Сергей Беляков. О «Генеральном плане Ост» Виктор Белкин. Гора и Рэм. (Фортамбек 1977 год)
Виктор Белкин. Гора и Рэм. (Фортамбек 1977 год) 8 июня Александр Лазарев
8 июня Александр Лазарев
